Vybrané partie z dátových štruktúr
2-INF-237, LS 2016/17
Vyhľadávanie kľúčových slov: Rozdiel medzi revíziami
Z VPDS
(→Tries (lexikograficke stromy)) |
(→Tries (lexikograficke stromy)) |
||
| Jedna medziľahlá revízia od jedného používateľa nie je zobrazená. | |||
| Riadok 86: | Riadok 86: | ||
'''Summary and implementations''' | '''Summary and implementations''' | ||
| − | * several words, total length D, alphabet size sigma, query size m | + | * several words, total length D, alphabet size sigma, query size m, number of words n |
* full array: memory O(D sigma), search O(m), insert all words O(D sigma) | * full array: memory O(D sigma), search O(m), insert all words O(D sigma) | ||
| − | * sorted array of variable size memory O(D), search O(m log sigma), add one word O(m log sigma + sigma), all words O(D log sigma + | + | * sorted array of variable size memory O(D), search O(m log sigma), add one word O(m log sigma + sigma), all words O(D log sigma + n sigma) |
* binary tree with letters as keywords: as before, but add only O(m log sigma) | * binary tree with letters as keywords: as before, but add only O(m log sigma) | ||
* hashing of alphabet: on average get rid of log sigma but many practical issues (resizing...) | * hashing of alphabet: on average get rid of log sigma but many practical issues (resizing...) | ||
| Riadok 136: | Riadok 136: | ||
k'=k; k=j+step; step*=2; | k'=k; k=j+step; step*=2; | ||
} | } | ||
| − | binary search in b[k'..k]; | + | binary search in b[k'..min(n,k)]; |
</pre> | </pre> | ||
* If k=j+x, doubling search needs O(log x) steps | * If k=j+x, doubling search needs O(log x) steps | ||
* Overall running time of the algorithm: doubling search at most m times, each time eliminates some number of elements x_i, time log(x1)+log(x2)+...log(xm) where x1+x2+...+xm<=n For what value of x_i is the sum is maximized? Happens for equally sized xi's, each n/m elements, <math>O(m\log(n/m))</math> time. For constant m logarithmic, for large m linear. Also better than simple merge if different clusters of similar values in each array. | * Overall running time of the algorithm: doubling search at most m times, each time eliminates some number of elements x_i, time log(x1)+log(x2)+...log(xm) where x1+x2+...+xm<=n For what value of x_i is the sum is maximized? Happens for equally sized xi's, each n/m elements, <math>O(m\log(n/m))</math> time. For constant m logarithmic, for large m linear. Also better than simple merge if different clusters of similar values in each array. | ||
* If more than 2 keywords, iterate (possibly starting with smallest lists - why better?), or extend the algorithm | * If more than 2 keywords, iterate (possibly starting with smallest lists - why better?), or extend the algorithm | ||
Aktuálna revízia z 15:00, 15. marec 2017
Predbežná verzia poznámok, nebojte sa upravovať: pripojiť informácie z prezentácie, pridať viac vysvetľujúceho textu a pod.
Obsah
Keyword search, inverted index, tries, set intersection
- uvod: slides
Full-text keyword search (Plnotextove vyhladavanie klucovych slov)
- definicia problemu: slides
- zacat diskusiu o tom, co treba indexovat
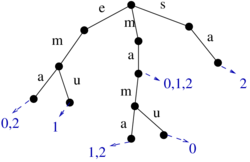
- Inverted index: for each word list the documents in which it appears.
Ema: 0,2 Emu: 1 ma: 0,1,2 Mama: 1,2 mamu: 0 sa: 2
- What data structures do we need:
- Map from words to lists (e.g. sorted array, binary search tree, hash)
- List of documents for each word (array or linked list)
- Budeme navrhovat riesenia a analyzovat zlozitost:
- cas predspracovania, cas na jeden dotaz
- Parametre: n pocet roznych slov, N celkovy pocet vyskytov (sucet dlzok zoznamov), m - max. dlzka slova, p - pocet najdenych vyskytov v danom dotaze, sigma - velkost abecedy
| Štruktúra | query | preprocessing |
|---|---|---|
| Utriedené pole | 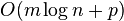
|
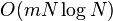
|
| Vyhľ. strom | 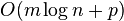
|
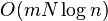
|
| Hašovanie - najh. prípad | 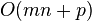
|
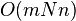
|
| Hašovanie - priem. prípad | 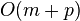
|
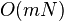
|
| Lex. strom | 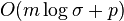
|
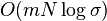 (neskor) (neskor)
|
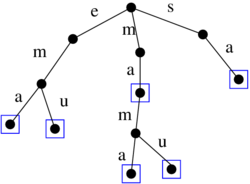
Tries (lexikograficke stromy)
- A different structure for storing a collection of words
- Edges from each node labeled with characters of the alphabet (0 to |Sigma| edges)
- Each node represents a string obtained by concatenation of characters on the edges
- If this string is in the collection, the node stores pointer to the list of occurrences (or other data)
- Small alphabet 0..sigma-1: in each node array of pointers child of length sigma-1, list of occurrences (possibly empty)
- Search for a word w of length m in the trie:
node = root;
for(i=0; i<m; i++) {
node = node->child[w[i]];
if(! node) return empty_list;
}
return node->list;
Time: O(m)
- Adding an occurrence of word w in document d to the trie:
node = root;
for(i=0; i<m; i++) {
if(! node->child[w[i]]) {
node->child[w[i]] = new node;
}
node = node->child[w[i]];
}
node->list.add(d)
Time: O(m) (assuming list addition in O(1))
Deletion of a word: what needs to be done (when do we delete a vertex), possibly a problem with deletion from list of occurrences
Summary and implementations
- several words, total length D, alphabet size sigma, query size m, number of words n
- full array: memory O(D sigma), search O(m), insert all words O(D sigma)
- sorted array of variable size memory O(D), search O(m log sigma), add one word O(m log sigma + sigma), all words O(D log sigma + n sigma)
- binary tree with letters as keywords: as before, but add only O(m log sigma)
- hashing of alphabet: on average get rid of log sigma but many practical issues (resizing...)
Multiple keywords
- Given several keywords, find documents that contain all of them (intersection, AND)
- Let us consider 2 keywords, one with m documents, other with n, m<n
- Assume that for each keyword we have a sorted array of occurrences (sorted e.g. by document ID, pagerank,...)
- Solution 1: Similar to merge in mergesort O(m+n) = O(n):
i=0; j=0;
while(i<m && j<n) {
if(a[i]==b[j]) { print a[i]; i++; j++; }
else if(a[i]<b[j]) { i++; }
else { j++; }
}
What if m<<n?
- do m times binary search
for(i=0; i<m; i++) {
k = binary_search(b, a[i])
if(a[i]==b[k]) print k;
}
- Rewrite a little bit to get an algorithm that generalizes the two (and possibly works faster)
j = 0; // current position in b
for(i=0; i<m; i++) {
find smallest k>=j s.t. b[k]>=a[i]; (*)
if(k==n) { break; }
j=k;
if(a[i]==b[j]) {
print a[i];
j++;
}
}
How to do (*):
- linear search k=j; while(k<n && b[k]<a[i]) { k++; } the same algorithm as before
- binary search in b[j..n]
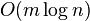 , faster for very small m
, faster for very small m
- doubling search/galloping search Bentley, Yao 1976 (general idea), Demaine, Lopez-Ortiz, Munro 2000 (application to intersection, more complex alg.), see also Baeza-Yates, Salinger (nice overview):
step = 1; k = j; k'=k;
while(k<n && b[k]<a[i]) {
k'=k; k=j+step; step*=2;
}
binary search in b[k'..min(n,k)];
- If k=j+x, doubling search needs O(log x) steps
- Overall running time of the algorithm: doubling search at most m times, each time eliminates some number of elements x_i, time log(x1)+log(x2)+...log(xm) where x1+x2+...+xm<=n For what value of x_i is the sum is maximized? Happens for equally sized xi's, each n/m elements,
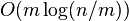 time. For constant m logarithmic, for large m linear. Also better than simple merge if different clusters of similar values in each array.
time. For constant m logarithmic, for large m linear. Also better than simple merge if different clusters of similar values in each array.
- If more than 2 keywords, iterate (possibly starting with smallest lists - why better?), or extend the algorithm