Vybrané partie z dátových štruktúr
2-INF-237, LS 2016/17
Sufixové stromy a polia: Rozdiel medzi revíziami
Z VPDS
| Riadok 6: | Riadok 6: | ||
[[Image:Suffix-gensuffix.png|250px]] | [[Image:Suffix-gensuffix.png|250px]] | ||
[[Image:Suffix-count.png|250px]] | [[Image:Suffix-count.png|250px]] | ||
| + | |||
| + | ==Suffix trees and applications== | ||
| + | ===Intro to suffix trees=== | ||
| + | * on slides | ||
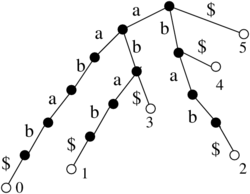
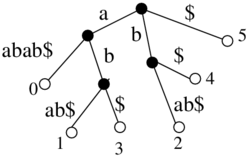
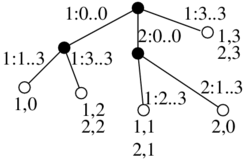
| + | ** example of generalized suffix tree for S1=aba$, S2=bba$ | ||
| + | * at the end: uses of suffix trees (assume we can build in O(n)) | ||
| + | ** string matching - build tree, then each pattern in O(m+k) - search through a subtree - its size? | ||
| + | ** find longest word that occurs twice in S - node with highest string depth O(n) | ||
| + | ** find longest word that is at least two strings in input set - node with highest string depth that has two different string represented - how to do details O(n) | ||
| + | ** next all maximal repeats | ||
| + | |||
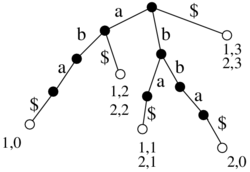
| + | ===Maximal pairs=== | ||
| + | * Definition, motivation on a slide | ||
| + | * example: S=xabxabyabz, max pairs xab-xab, ab-ab (2x) | ||
| + | * Each maximal repeat is an internal node (cannot end in the middle of an edge). Why? | ||
| + | * Let v is a leaf for suffix S[i..n-1], let l(v)=S[i-1] - left character | ||
| + | * Def. Node v is diverse (roznorody) if its subtree contains leaves labeled by at least 2 different values of l(v) | ||
| + | * Theorem. Node v corresponds to a maximal repeat <=> v is diverse | ||
| + | * Proof: => obvious. | ||
| + | * <= Let v corresponds to string A | ||
| + | * v is diverse => xA, yA are substrings in S for some x!=y | ||
| + | * v is a node => Ap, Aq are substrings in S for some p!=q | ||
| + | * If xA is always followed by the same character, e.g. p, then Aq must be preceded by some z!=x, we have pairs xAp, zAq | ||
| + | * Otherwise we have xA is followed by at least 2 different characters, say p and q. If yAp in S, use maximal pairs yAp, xAq, otherwise use maximal pairs xAp, yA? | ||
| + | |||
| + | Summary | ||
| + | * create suffix tree for #S$ | ||
| + | * compute l(v) for each leaf | ||
| + | * compute diversity of nodes in a bottom-up fashion | ||
| + | * print all substrings (their indices) corresponding to diverse nodes | ||
| + | Further extensions: find only repeats which are not parts of other repeats, finding all maximal pairs,... | ||
| + | |||
| + | ===LCA v sufixovych stromoch=== | ||
| + | * def na slajde | ||
| + | * majme listy zodpovedajuce sufixom S[i..n-1] a S[j..n-1] | ||
| + | * lca(u,v) = najdlhsi spolocny prefix S[i..n-1] a S[j..n-1] | ||
| + | * funguje aj v zovseobecnenych sufixovych stromoch, vtedy sufixy mozu byt z roznych retazcov | ||
| + | |||
| + | ===Aproximate string matching=== | ||
| + | * on slides, do running time analysis O(nk) | ||
| + | * wildcards | ||
| + | |||
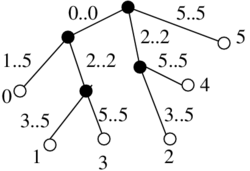
| + | ===Counting documents=== | ||
| + | * list of leaves in DFS order | ||
| + | * each subtree an interval of the list | ||
| + | * separate to sublists: L_i = list of suffixes of S_i in pre-order | ||
| + | * compute lca for each two consecutive members of each L_i | ||
| + | * in each node counter h(v): how many times found as lca | ||
| + | * compute in each node l(v): number of leaves in subtree, s(v): sum of h(v) in subtree | ||
| + | * C(v) = l(v)-s(v) | ||
| + | Proof: | ||
| + | * consider node v and string Si | ||
| + | * if Si occurs k>0 times in subtree of v, it should be counted once in c(v) | ||
| + | ** counted k-times in l(v), k-1 times in s(v) | ||
| + | * if Si not in subtree of v, it should be counted 0 times | ||
| + | ** counted 0 times in both l(v) and s(v) | ||
| + | |||
==Literatúra== | ==Literatúra== | ||
* Dan Gusfield (1997) [http://www.cambridge.org/uk/catalogue/catalogue.asp?isbn=0521585198 Algorithms on Strings, Trees and Sequences: Computer Science and Computational Biology.] Cambridge University Press. Prezenčne v knižnici so signatúrou I-INF-G-8. | * Dan Gusfield (1997) [http://www.cambridge.org/uk/catalogue/catalogue.asp?isbn=0521585198 Algorithms on Strings, Trees and Sequences: Computer Science and Computational Biology.] Cambridge University Press. Prezenčne v knižnici so signatúrou I-INF-G-8. | ||
* Poznámky z predmetu Vyhľadávanie v texte [http://compbio.fmph.uniba.sk/vyuka/vvt/poznamky/main-2013-05-20.pdf] (zčasti písané študentami a nedokončené) | * Poznámky z predmetu Vyhľadávanie v texte [http://compbio.fmph.uniba.sk/vyuka/vvt/poznamky/main-2013-05-20.pdf] (zčasti písané študentami a nedokončené) | ||
Verzia zo dňa a času 13:44, 25. marec 2014
Obsah
Suffix trees and applications
Intro to suffix trees
- on slides
- example of generalized suffix tree for S1=aba$, S2=bba$
- at the end: uses of suffix trees (assume we can build in O(n))
- string matching - build tree, then each pattern in O(m+k) - search through a subtree - its size?
- find longest word that occurs twice in S - node with highest string depth O(n)
- find longest word that is at least two strings in input set - node with highest string depth that has two different string represented - how to do details O(n)
- next all maximal repeats
Maximal pairs
- Definition, motivation on a slide
- example: S=xabxabyabz, max pairs xab-xab, ab-ab (2x)
- Each maximal repeat is an internal node (cannot end in the middle of an edge). Why?
- Let v is a leaf for suffix S[i..n-1], let l(v)=S[i-1] - left character
- Def. Node v is diverse (roznorody) if its subtree contains leaves labeled by at least 2 different values of l(v)
- Theorem. Node v corresponds to a maximal repeat <=> v is diverse
- Proof: => obvious.
- <= Let v corresponds to string A
- v is diverse => xA, yA are substrings in S for some x!=y
- v is a node => Ap, Aq are substrings in S for some p!=q
- If xA is always followed by the same character, e.g. p, then Aq must be preceded by some z!=x, we have pairs xAp, zAq
- Otherwise we have xA is followed by at least 2 different characters, say p and q. If yAp in S, use maximal pairs yAp, xAq, otherwise use maximal pairs xAp, yA?
Summary
- create suffix tree for #S$
- compute l(v) for each leaf
- compute diversity of nodes in a bottom-up fashion
- print all substrings (their indices) corresponding to diverse nodes
Further extensions: find only repeats which are not parts of other repeats, finding all maximal pairs,...
LCA v sufixovych stromoch
- def na slajde
- majme listy zodpovedajuce sufixom S[i..n-1] a S[j..n-1]
- lca(u,v) = najdlhsi spolocny prefix S[i..n-1] a S[j..n-1]
- funguje aj v zovseobecnenych sufixovych stromoch, vtedy sufixy mozu byt z roznych retazcov
Aproximate string matching
- on slides, do running time analysis O(nk)
- wildcards
Counting documents
- list of leaves in DFS order
- each subtree an interval of the list
- separate to sublists: L_i = list of suffixes of S_i in pre-order
- compute lca for each two consecutive members of each L_i
- in each node counter h(v): how many times found as lca
- compute in each node l(v): number of leaves in subtree, s(v): sum of h(v) in subtree
- C(v) = l(v)-s(v)
Proof:
- consider node v and string Si
- if Si occurs k>0 times in subtree of v, it should be counted once in c(v)
- counted k-times in l(v), k-1 times in s(v)
- if Si not in subtree of v, it should be counted 0 times
- counted 0 times in both l(v) and s(v)
Literatúra
- Dan Gusfield (1997) Algorithms on Strings, Trees and Sequences: Computer Science and Computational Biology. Cambridge University Press. Prezenčne v knižnici so signatúrou I-INF-G-8.
- Poznámky z predmetu Vyhľadávanie v texte [1] (zčasti písané študentami a nedokončené)