Vybrané partie z dátových štruktúr
2-INF-237, LS 2016/17

Úvod · Pravidlá · Prednášky · Prezentácia · Ako poznámkovať · Moodle
Táto stránka sa týka školského roku 2016/17. V školskom roku 2017/18 predmet vyučuje Jakub Kováč, stránku predmetu je https://people.ksp.sk/~kuko/ds


Hešovanie: Rozdiel medzi revíziami

Z VPDS
Prejsť na: navigácia, hľadanie
(→‎Bloom Filter (Bloom 1970))
(→‎Minimum hashing)
Riadok 199: Riadok 199:
  
  
−
===Minimum hashing===
+
==Minimum hashing==
 
* similarity of two sets measured as Jaccard index J(A,B) = |A intersect B | / | A union B |
 
* similarity of two sets measured as Jaccard index J(A,B) = |A intersect B | / | A union B |
 
* distance d(A,B) = 1-J(A,B)
 
* distance d(A,B) = 1-J(A,B)

Verzia zo dňa a času 16:01, 13. apríl 2016

Introduction to hashing

  • Universe U = {0,..., u-1}
  • Table of size m
  • Hash function h : U -> {0,...,m-1}
  • Let X be the set of elements currently in the hash table, n = |X|
  • We will assume n = Theta(m)

Totally random hash function

  • (a.k.a uniform hashing model)
  • select hash value h(x) for each x in U uniformly independently
  • not practical - storing this hash function requires u * lg m bits
  • used for simplified analysis of hashing in ideal case

Universal family of hash functions

  • some set of functions H
  • draw a fuction h uniformly randomly from H
  • there is a constant c such that for any distinct x,y from U we have Pr(h(x) = h(y)) <= c/m
  • probability goes over choices of h

Note

  • for totally random hash function, this probability is exactly 1/m

Example of a universal family:

  • choose a fixed prime p >= u
  • H_p = { h_a | h_a(x) =(ax mod p) mod m), 1<=a<=p-1 }
  • p-1 hash functions, parameter a chosen randomly

Proof of universality

  • consider x!=y, both from U
  • if they collide (ax mod p) mod m = (ay mod p) mod m
  • let c = (ax mod p), d = (ay mod p)
  • note that c,d in {0..p-1}
  • also c!=d because otherwise a(x-y) is divisible by p and both a and |x-y| are numbers from {1,...,p-1} and p is prime
  • since c mod m = d mod m, then c-d = qm where 0<|qm|<p
  • there are <=2(p-1)/m choices of q where |qm|<p
  • we get a(x-y) mod p = qm mod p
  • this has exactly one solution a in {1...p-1}
    • if there were two solutions a1 and a2, then (a1-a2)(x-y_ would be divisible by p, which is again not possible
  • overall at most 2(p-1)/m choices of hash functions collide x and y
  • out of p-1 all hash functions in H_p
  • therefore probability of collision <=2/m

Hashing with chaining, using universal family of h.f.

  • linked list (or vector) for each hash table slot
  • let c_i be the length of chain i
  • consider element x from U, let i = h(x)
  • any element y from X s.t. x!=y maps to i with probability <= c/m
  • so E[c_i] <= 1 + n * c / m = O(1)
    • from linearity of expectation - sum over indicator variables for each y in X if it collides with x
    • +1 in case x is in X
  • so expected time of any search, insert and delete is O(1)
    • again, expectation taken over random choice of h from universal H
  • however, what is the expected length of the longest chain in the table?
    • O(1+ sqrt(n^2 / m)) = O(sqrt(n))
    • see Brass, p. 382
    • there is a matching lower bound
  • for totally random hash function this is "only" O(log n / log log n)
  • similar bound proved also for some more realistic families of hash functions
  • so the worst-case query is on average close to logarithmic

References

Perfect hashing

Static case

  • Fredman, Komlos, Szemeredi 1984
  • avoid any collisions, O(1) search in a static set
  • two-level scheme: use a universal hash function to hash to a table of size m = Theta(n)
  • each bucket i with set of elements X_i of size c_i hashed to a second-level hash of size m_i = alpha c_i^2 for some constant alpha
  • again use a universal hash function for each second-level hash
  • expected total number of collisions in a second level for slot i:
    • sum_{u,v in X_i, u!=v} Pr(h(u) = h(v)) <= (c_i)^2 c/m_i = c/alpha = O(1)
    • here c is the constant from definition universal family
  • with a sufficently large alpha this expected number of collisions is <=1/2
    • e.g. for c = 2 set alpha = 4
  • then with probability >=1/2 no collisions by Markov inequality
    • number of collisions is a random variable Y number with possible values 0,1,2,...
    • if E[Y]<=1/2, Pr(Y>=1)<=1/2 and thus Pr(Y=0)>=1/2
  • when building a hash table if we get a collision, randomly sample another hash function
  • in O(1) expected trials get a good hash function
  • expected space: m + sum_i m_i^2 = Theta(m + sum_i c_i^2)
  • sum_i (c_i^2) is the number pairs (x,y) s.t. x,y in X and h(x)=h(y); include x=y
  • sum_{x,y} Pr(h(x)=h(y)) = n + sum_{x!=y} Pr(h(x)=h(y)) = n + n^2 c / m = Theta(n)
  • so expected space is linear
  • can be made worst-case by repeating construction if memory too big
  • expected construction time O(n)

Dynamic perfect hashing

  • amortized vector-like tricks
  • when a 2-nd level hash table get too full, allocate a bigger one
  • O(1) deterministic search
  • O(1) amortized expectd update
  • O(n) expected space

References

Bloom Filter (Bloom 1970)

  • supports insert x, test if x is in the set
    • may give false positives, e.g. claim that x is in the set when it is not
    • false negatives do not occur

Algorithm

  • a bit string B[0,...,m-1] of length m, and k hash functions hi : U -> {0, ..., m-1}.
  • insert(x): set bits B[h1(x)], ..., B[hk(x)] to 1.
  • test if x in the set: compute h1(y), ..., hk(y) and check whether all these bits are 1
    • if yes, claim x is in the set, but possibility of error
    • if no, answer no, surely true

Bounding the error If hash functions are totally random and independent, the probability of error is approximately (1-exp(-nk/m))^k

  • in fact probability somewhat higher for smaller values
  • proof of the bound later
  • totally random hash functions impractical (need to store hash value for each element of the universe), but the assumption simplifies analysis
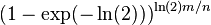  • if we set k = ln(2) m/n, get error (1-\exp(-\ln(2)))^{{\ln(2)m/n}}.
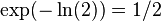  • \exp(-\ln(2))=1/2 and thus we get error 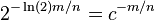2^{{-\ln(2)m/n}}=c^{{-m/n}}, where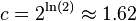 c=2^{{\ln(2)}}\approx 1.62
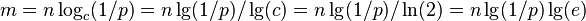
  • to get error rate p for some n, we need m=n\log _{c}(1/p)=n\lg(1/p)/\lg(c)=n\lg(1/p)/\ln(2)=n\lg(1/p)\lg(e)
  • for 1% error, we need about m=10n bits of space and k=7
  • memory size and error rate are independent of the size of the universe U
  • compare to a hash table, which needs at least to store data items themselves (e.g. in n lg u bits)
  • if we used k=1 (Bloom filter with one hash function), we need m=n/ln(1/(1-p)) bits, which for p=0.01 is about 99.5n, about 10 times more than with 7 hash functions

Use of Bloom filters

  • e.g. an approximate index of a larger data structure on a disk - if x not in the filter, do not bother looking at the disk, but small number of false positives not a problem
  • Example: Google BigTable maps row label, column label and timestamp to a record, underlies many Google technologies. It uses Bloom filter to check if a combination of row and column label occur in a given fragment of the table
    • For details, see Chang, Fay, et al. "Bigtable: A distributed storage system for structured data." ACM Transactions on Computer Systems (TOCS) 26.2 (2008): 4. [1]
  • see also A. Z. Broder and M. Mitzenmacher. Network applications of Bloom filters: A survey. In Internet Math. Volume 1, Number 4 (2003), 485-509. [2]

Proof of the bound

  • probability that some B[i] is set to 1 by hj(x) is 1/m
  • probability that B[i] is not set to 1 is therefore 1-1/m and since we use k independent hash functions, the probability that B[i] is not set to one by any of them is (1-1/m)^k
  • if we insert n elements, each is hashed by each function independently of other elements (hash functions are random) and thus Pr(B[i]=0)=(1-1/m)^{nk}
  • Pr(B[i]=1) = 1-Pr(B[i]=0)
  • consider a new element y which is not in the set
  • error occurs when B[hj(y)]==1 for all j=1..k
  • assume for now that these events are independent for different j
  • error then occurs with probability Pr(B[i]=1)^k = (1-(1-1/m)^{nk})^k
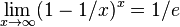
  • recall that \lim _{{x\to \infty }}(1-1/x)^{x}=1/e
  • thus probability of error is approximately (1-exp(-nk/m))^k

However, Pr(B[i]=1) are not independent

  • consider the following experiment: have 2 binary random variables Y1, Y2, each generated independently, uniformly (i.e. P(Y1=1) = 0.5)
  • Let X1 = Ya and X2 = Yb where a and b are chosen independently uniformly from set {1,2}
  • X1 and X2 are not independent, e.g. Pr(X2 = 1|X1 = 1) = 2/3, whereas Pr(X2=1) = 1/2. (check the constants!)
  • note: X1 and X2 would be independent conditioned on the sum of Y1+Y2.
  • In Mitzenmacher & Upfal (2005), pp. 109–111, 308. - less strict independence assumption

Exercise Let us assume that we have separate Bloom filters for sets A and B with the same set k hash functions. How can we create Bloom filters for union and intersection? Will the result be different from filter created directly for the union or for the intersection?

Theory

  • Bloom filter above use about 1.44 n lg(1/p) bits to achieve error rate p. There is lower bound of n lg(1/p) [Carter et al 1978], constant 1.44 can be improved to 1+o(1) using more complex data structures, which are then probably less practical
  • Pagh, Anna, Rasmus Pagh, and S. Srinivasa Rao. "An optimal Bloom filter replacement." SODA 2005. [3]
  • L. Carter, R. Floyd, J. Gill, G. Markowsky, and M. Wegman. Exact and approximate membership testers. STOC 1978, pages 59–65. [4]
  • see also proof of lower bound in Broder and Mitzenmacher 2003 below

Counting Bloom filters

  • support insert and delete
  • each B[i] is a counter with b bits
  • insert increases counters, decrease decreases
  • assume no overflows, or reserve largest value 2^b-1 as infinity, cannot be increased or decreased
  • Fan, Li, et al. "Summary cache: A scalable wide-area web cache sharing protocol." ACM SIGCOMM Computer Communication Review. Vol. 28. No. 4. ACM, 1998. [5]

References

Locality Sensitive Hashing

  • todo: expand and according to slides
  • typical hashing tables used for exact search: is x in set X?
  • nearest neighbor(x): find y in set X minimizing d(x,y) for a given distance measure d
    • or given x and distance threshold r, find all y in X with d(x,y)<=r
  • want: polynomial time preprocessing of X, polylogarithmic queries
  • later in the course: geometric data structures for similar problems in R^2 or higher dimensions
  • but time or space grows exponentially with dimension (alternative is linear search) - "curse of dimensionality"
  • examples of high-dimensional objects: images, documents, etc.
  • locality sensitive hashing (LHS) is a randomized data structure not guaranteed to find the best answer but better running time

Approximate near neighbour (r,c)-NN

  • preprocess a set X of size n for given r,c
  • query(x):
    • if there is y in X such that d(y,x)<=r, return z in X such that d(z,x)<=c*r
    • LHS returns such z with some probability at least f

Example for Hamming distance in binary strings of length d

  • Hash each string using L hashing functions, each using O(log n) randomly chosen string positions (hidden constant depends on d, r, c), then rehash using some other hash function to tables of size O(n) or a single table of size O(nL)
  • Given q, find it using all L hash function, check every collision, report if distance at most cr. If checked more than 3L collisions, stop.
  • L = O(n^{1/c})
  • Space O(nL + nd), query time O(Ld+L(d/r)log n)
  • Probability of failure less than some constant f < 1, can be boosted by repeating independently


Minimum hashing

  • similarity of two sets measured as Jaccard index J(A,B) = |A intersect B | / | A union B |
  • distance d(A,B) = 1-J(A,B)
  • used e.g. for approximate duplicate document detection based on set of words occurring in the document
  • choose a totally random hash function h
  • minhash_h(A) = \min_{x\in A} h(x)
  • Pr(minhash_h(A)=minhash_h(B)) = J(A,B) = 1-d(A,B) if using totally random hash function an no collisions in A union B
    • where can be minimum in union? if in intersection, we get equality, otherwise not
  • (r_1, r_2, 1-r_1, 1-r_2)-sensitive family (if we assume no collisions)
  • again can we apply amplification

Sources

Zdroj: „http://compbio.fmph.uniba.sk/vyuka/vpds/index.php?title=Hešovanie&oldid=512“