Hešovanie: Rozdiel medzi revíziami

Verzia zo dňa a času 14:04, 29. apríl 2015

Zdroje

Prednaska L10 Erika Demaina z MIT: http://courses.csail.mit.edu/6.851/spring12/lectures/
Článok z Wikipédia o Bloom filtroch http://en.wikipedia.org/wiki/Bloom_filter
Učebnica Brass 2008 Advanced data structures (Bloom filters)

Osnova

vlastnosti hešovacích funkcií: totally random, universal, k-wise independent, simple tabulation;
chaining, perfect hashing, linear probing,
Bloom filters, locality sensitive hashing

V sylabe na skúšku je len perfect hashing, rozoberané na Erikovej prednáške

Bloom Filter (Bloom 1970)

supports insert x, test if x is in the set
- may give false positives, e.g. claim that x is in the set when it is not
- false negatives do not occur

Algorithm

a bit string B[0,...,m-1] of length m, and k hash functions hi : U -> {0, ..., m-1}.
insert(x): set bits B[h1(x)], ..., B[hk(x)] to 1.
test if x in the set: compute h1(y), ..., hk(y) and check whether all these bits are 1
- if yes, claim x is in the set, but possibility of error
- if no, answer no, surely true

Lemma: If hash functions are totally random and independent, the probability of error is at most (1-exp(-nk/m))^k

proof later
totally random hash functions impractical (need to store hash value for each element of the universe), but the assumption simplifies analysis
if we set k = ln(2) m/n, get error 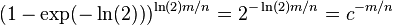$(1-\exp(-\ln(2)))^{{\ln(2)m/n}}=2^{{-\ln(2)m/n}}=c^{{-m/n}}$ , where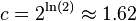 $c=2^{{\ln(2)}}\approx 1.62$
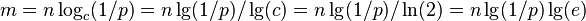
to get error rate p for some n, we need $m=n\log _{c}(1/p)=n\lg(1/p)/\lg(c)=n\lg(1/p)/\ln(2)=n\lg(1/p)\lg(e)$
for 1% error, we need about m=10n bits of space and k=7
memory size and error rate are independent of the size of the universe U
compare to a hash table, which needs at least to store data items themselves (e.g. in n lg u bits)
if we used k=1 (Bloom filter with one hash function), we need m=n/ln(1/(1-p)) bits, which for p=0.01 is about 99.5n, about 10 times more than with 7 hash functions

Use of Bloom filters

e.g. an approximate index of a larger data structure on a disk - if x not in the filter, do not bother looking at the disk, but small number of false positives not a problem
Example: Google BigTable maps row label, column label and timestamp to a record, underlies many Google technologies. It uses Bloom filter to check if a combination of row and column label occur in a given fragment of the table
- For details, see Chang, Fay, et al. "Bigtable: A distributed storage system for structured data." ACM Transactions on Computer Systems (TOCS) 26.2 (2008): 4. [1]
see also A. Z. Broder and M. Mitzenmacher. Network applications of Bloom filters: A survey. In Internet Math. Volume 1, Number 4 (2003), 485-509. [2]

Proof of lemma

probability that some B[i] is set to 1 by hj(x) is 1/m
probability that B[i] is not set to 1 is therefore 1-1/m and since we use k independent hash functions, the probability that B[i] is not set to one by any of them is (1-1/m)^k
if we insert n elements, each is hashed by each function independently of other elements (hash functions are random) and thus Pr(B[i]=0)=(1-1/m)^{nk}
Pr(B[i]=1) = 1-Pr(B[i]=0)
consider a new element y which is not in the set
error occurs when B[hj(y)]==1 for j=1..k,
this happens with probability Pr(B[i]=1)^k = (1-(1-1/m)^{nk})^k
recall that for x>1 we have (1-1/x)^x < 1/e (equality in limit as x->infinity)
thus probability of error <= (1-exp(-nk/m))^k

!check Mitzenmacher & Upfal (2005), pp. 109–111, 308. - less strict independence assumption

Exercise Let us assume that we have separate Bloom filters for sets A and B with the same set k hash functions. How can we create Bloom filters for union and intersection? Will the result be different from filter created directly for the union or for the intersection?

Theory

Bloom filter above use about 1.44 n lg(1/p) bits to achieve error rate p. There is lower bound of n lg(1/p) [Carter et al 1978], constant 1.44 can be improved to 1+o(1) using more complex data structures, which are then probably less practical
Pagh, Anna, Rasmus Pagh, and S. Srinivasa Rao. "An optimal Bloom filter replacement." SODA 2005. [3]
L. Carter, R. Floyd, J. Gill, G. Markowsky, and M. Wegman. Exact and approximate membership testers. STOC 1978, pages 59–65. [4]
see also proof of lower bound in Broder and Mitzenmacher 2003 below

Counting Bloom filters

support insert and delete
each B[i] is a counter with b bits
insert increases counters, decrease decreases
assume no overflows, or reserve largest value 2^b-1 as infinity, cannot be increased or decreased
Fan, Li, et al. "Summary cache: A scalable wide-area web cache sharing protocol." ACM SIGCOMM Computer Communication Review. Vol. 28. No. 4. ACM, 1998. [5]

References

Bloom, Burton H. (1970), "Space/Time Trade-offs in Hash Coding with Allowable Errors", Communications of the ACM 13 (7): 422–426
Bloom filter. In Wikipedia, The Free Encyclopedia. Retrieved January 17, 2015, from http://en.wikipedia.org/w/index.php?title=Bloom_filter&oldid=641921171
A. Z. Broder and M. Mitzenmacher. Network applications of Bloom filters: A survey. In Internet Math. Volume 1, Number 4 (2003), 485-509. [6]

Locality Sensitive Hashing

Har-Peled, Sariel, Piotr Indyk, and Rajeev Motwani. "Approximate Nearest Neighbor: Towards Removing the Curse of Dimensionality." Theory of Computing 8.1 (2012): 321-350.
- Proprocess: A set P of n binary sequences of length k, radius r, gap c
- Query: binary sequence q of length q
- Output: If there exist a sequence within Hamming distance r from q, find a sequence within r*c of q with probability at least f.
- Hash each point in P using L hashing functions, each using O(log n) randomly chosen sequence positions (hidden constant depends on d, r, c), put all results to bins in one table
- Given q, find it using all L hash function, check every collision, report if distance at most cr. If checked more than 3L collisions, stop.
- L = O(n^{1/c})
- Space O(nL), query time O(Ld+L(d/r)log n)
- Probability of failure less than some constant < 1, can be boosted by repeating independently

@@ Riadok 11: / Riadok 11: @@
 V sylabe na skúšku je len perfect hashing, rozoberané na Erikovej prednáške
-===Bloom Filter (1970)===
+===Bloom Filter (Bloom 1970)===
-* a bit string of length b, and k hash functions hi : U -> {1, . . . , b}.
+* supports insert ''x'', test if ''x'' is in the set
-* insert(x): set bits h1 (x), . . . , hk (x) to 1.
+** may give false positives, e.g. claim that ''x'' is in the set when it is not
-* test if x in the set: compute h1 (y), . . . , hk (y) and check whether all these bits are 1
+** false negatives do not occur
+'''Algorithm'''
+* a bit string B[0,...,m-1] of length m, and k hash functions hi : U -> {0, ..., m-1}.
+* insert(x): set bits B[h1(x)], ..., B[hk(x)] to 1.
+* test if x in the set: compute h1(y), ..., hk(y) and check whether all these bits are 1
 ** if yes, claim x is in the set, but possibility of error
 ** if no, answer no, surely true
-Lemma: if hash functions totally random and independent and  b = lg(e)kn bits, error is at most 2^{−k}.
+'''Lemma:''' If hash functions are totally random and independent, the probability of error is at most (1-exp(-nk/m))^k
 * proof later
-* totally random hash function impractical (need to store hash value for each element of the universe)
+* totally random hash functions impractical (need to store hash value for each element of the universe), but the assumption simplifies analysis
-* error independent of the size of the universe U
+* if we set k = ln(2) m/n, get error <math>(1-\exp(-\ln(2)))^{\ln(2)m/n} = 2^{-\ln(2)m/n} = c^{-m/n}</math>, where <math>c = 2^{\ln(2)} \approx 1.62</math>
-* lg(e) is approx 1.44. for 1% error, k=7, about 10 bits per element
+* to get error rate p for some n, we need <math>m = n \log_c (1/p) = n \lg(1/p)/\lg(c) = n \lg(1/p)/\ln(2) = n \lg(1/p) \lg(e)</math>
-* compare to a hash table, which needs at lead n lg u bits to store data items themselves
+* for 1% error, we need about m=10n bits of space and k=7
+* memory size and error rate are independent of the size of the universe U
-Use of Bloom filters
+* compare to a hash table, which needs at least to store data items themselves (e.g. in n lg u bits)
+* if we used k=1 (Bloom filter with one hash function), we need m=n/ln(1/(1-p)) bits, which for p=0.01 is about 99.5n, about 10 times more than with 7 hash functions
+'''Use of Bloom filters'''
 * e.g. an approximate index of a larger data structure on a disk - if x not in the filter, do not bother looking at the disk, but small number of false positives not a problem
+* Example: Google BigTable maps row label, column label and timestamp to a record, underlies many Google technologies. It uses Bloom filter to check if a combination of row and column label occur in a given fragment of the table
+** For details, see Chang, Fay, et al. "Bigtable: A distributed storage system for structured data." ACM Transactions on Computer Systems (TOCS) 26.2 (2008): 4. [http://static.usenix.org/events/osdi06/tech/chang/chang_html/?em_x=22]
+* see also A. Z. Broder and M. Mitzenmacher. Network applications of Bloom filters: A survey. In Internet Math. Volume 1, Number 4 (2003), 485-509. [http://projecteuclid.org/download/pdf_1/euclid.im/1109191032]
+'''Proof of lemma'''
+* probability that some B[i] is set to 1 by hj(x) is 1/m
+* probability that B[i] is not set to 1 is therefore 1-1/m and since we use k independent hash functions, the probability that B[i] is not set to one by any of them is (1-1/m)^k
+* if we insert n elements, each is hashed by each function independently of other elements (hash functions are random) and thus Pr(B[i]=0)=(1-1/m)^{nk}
+* Pr(B[i]=1) = 1-Pr(B[i]=0)
+* consider a new element y which is not in the set
+* error occurs when B[hj(y)]==1 for j=1..k,
+* this happens with probability Pr(B[i]=1)^k = (1-(1-1/m)^{nk})^k
+* recall that for x>1 we have (1-1/x)^x < 1/e (equality in limit as x->infinity)
+* thus probability of error <= (1-exp(-nk/m))^k
+!check Mitzenmacher & Upfal (2005), pp. 109–111, 308. - less strict independence assumption
+'''Exercise'''
+Let us assume that we have separate Bloom filters for sets A and B with the same set k hash functions. How can we create Bloom filters for union and intersection? Will the result be different from filter created directly for the union or for the intersection?
+'''Theory'''
+* Bloom filter above use about 1.44 n lg(1/p) bits to achieve error rate p. There is lower bound of n lg(1/p) [Carter et al 1978], constant 1.44 can be improved to 1+o(1) using more complex data structures, which are then probably less practical
+* Pagh, Anna, Rasmus Pagh, and S. Srinivasa Rao. "An optimal Bloom filter replacement." SODA 2005. [http://www.itu.dk/~annao/Publications/Filter.pdf]
+* L. Carter, R. Floyd, J. Gill, G. Markowsky, and M. Wegman. Exact and approximate membership testers. STOC 1978, pages 59–65. [http://www.researchgate.net/publication/234830711_Exact_and_approximate_membership_testers/file/e0b4951d5595258a88.pdf]
+* see also proof of lower bound in Broder and Mitzenmacher 2003 below
-Proof of lemma
+'''Counting Bloom filters'''
+* support insert and delete
+* each B[i] is a counter with b bits
+* insert increases counters, decrease decreases
+* assume no overflows, or reserve largest value 2^b-1 as infinity, cannot be increased or decreased
+* Fan, Li, et al. "Summary cache: A scalable wide-area web cache sharing protocol." ACM SIGCOMM Computer Communication Review. Vol. 28. No. 4. ACM, 1998. [https://www.cs.princeton.edu/courses/archive/spring05/cos598E/bib/p254-fan.pdf]
-References
+'''References'''
 * Bloom, Burton H. (1970), [http://dx.doi.org/10.1145%2F362686.362692 "Space/Time Trade-offs in Hash Coding with Allowable Errors"], Communications of the ACM 13 (7): 422–426
 * Bloom filter. In Wikipedia, The Free Encyclopedia. Retrieved January 17, 2015, from http://en.wikipedia.org/w/index.php?title=Bloom_filter&oldid=641921171
+* A. Z. Broder and M. Mitzenmacher. Network applications of Bloom filters: A survey. In Internet Math. Volume 1, Number 4 (2003), 485-509. [http://projecteuclid.org/download/pdf_1/euclid.im/1109191032]
 ===Locality Sensitive Hashing===

Hešovanie: Rozdiel medzi revíziami

Verzia zo dňa a času 14:04, 29. apríl 2015

Bloom Filter (Bloom 1970)

Locality Sensitive Hashing

Navigačné menu

Osobné nástroje

Menné priestory

Varianty

Zobrazení

Operácie

Hľadať

Navigácia

Nástroje