Vybrané partie z dátových štruktúr
2-INF-237, LS 2016/17
Hešovanie: Rozdiel medzi revíziami
(→Bloom Filter (Bloom 1970)) |
|||
| Riadok 2: | Riadok 2: | ||
* Prednaska L10 Erika Demaina z MIT: http://courses.csail.mit.edu/6.851/spring12/lectures/ | * Prednaska L10 Erika Demaina z MIT: http://courses.csail.mit.edu/6.851/spring12/lectures/ | ||
* Článok z Wikipédia o Bloom filtroch http://en.wikipedia.org/wiki/Bloom_filter | * Článok z Wikipédia o Bloom filtroch http://en.wikipedia.org/wiki/Bloom_filter | ||
| − | * Učebnica Brass 2008 Advanced data structures | + | * Učebnica Brass 2008 Advanced data structures |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ===Introduction to hashing=== | |
| + | |||
| + | * Universe U = {0,..., u-1} | ||
| + | * Table of size m | ||
| + | * Hash function h : U -> {0,...,m-1} | ||
| + | * Let T be the set of elements currently in the hash table, n = |T| | ||
| + | * We will assume n = Theta(m) | ||
| + | |||
| + | Totally random hash function (a.k.a uniform hashing model) | ||
| + | * select hash value h(x) for each x in U uniformy independently | ||
| + | * not practical - storing this hash function requires u * lg m bits | ||
| + | * used for simplified analysis of hashing in ideal case | ||
| + | |||
| + | Universal family of hash functions | ||
| + | * some set of functions H | ||
| + | * draw a fuction h uniformly randomly from H | ||
| + | * there is a constant c such that for any distinct u,v from U we have Pr(h(u) = h(v)) <= c/m | ||
| + | * probability goes over choices of h | ||
| + | |||
| + | Note | ||
| + | * for totally random hash function, this probability is exactly 1/m | ||
| + | |||
| + | Example of a universal family: | ||
| + | * choose a fixed prime p >= u | ||
| + | * H_p = { h_a | h_a(x) =(ax mod p) mod m), 1<=a<=p-1 } | ||
| + | * p-1 hash functions, parameter a chosen randomly | ||
| + | |||
| + | Proof of universality | ||
| + | * consider x!=y, both from U | ||
| + | * if they collide (ax mod p) mod m = (ay mod p) mod m | ||
| + | * let c = (ax mod p), d = (ay mod p) | ||
| + | * note that c,d in {0..p-1} | ||
| + | * also c!=d because otherwise a(x-y) is divisible by p and both a and |x-y| are numbers from {1,...,p-1} and p is prime | ||
| + | * since c mod m = d mod m, then c-d = qm where 0<|qm|<p | ||
| + | * there are <=2(p-1)/m choices of q where |qm|<p | ||
| + | * we get a(x-y) mod p = qm mod p | ||
| + | * this has exactly one solution a in {0...p-1} | ||
| + | * overall at most 2(p-1)/m choices of hash functions collide x and y | ||
| + | * out of p-1 all hash functions in H_p | ||
| + | * therefore probability of collision <=2/m | ||
| + | |||
| + | |||
| + | Hashing with chaining, using universal family of h.f. | ||
| + | * linked list (or vector) for each hash table slot | ||
| + | * let c_i be the length of chain i | ||
| + | * consider element u from U, let i = h(u) | ||
| + | * any element x from T s.t. u!=x maps to i with probability <= c/m | ||
| + | * so E[c_i] <= 1 + n * c / m = O(1) | ||
| + | ** from linearity of expectation - sum over indicator variables for each x in T if it collides with u | ||
| + | ** +1 in case u is in T | ||
| + | * so expected time of any search, insert and delete is O(1) | ||
| + | ** again, expectation taken over random choice of h from universal H | ||
| + | * however, what is the expected length of the longest chain in the table? | ||
| + | ** O(1+ sqrt(n^2 / m)) = O(sqrt(n)) | ||
| + | ** see Brass, p. 382 | ||
| + | ** there is a matching lower bound | ||
| + | * for totally random hash function this is "only" O(log n / log log n) | ||
| + | * similar bound proved also for some more realistic families of hash functions | ||
| + | * so the worst-case query is on average close to logarithmic | ||
| + | |||
| + | ===Perfect hashing=== | ||
| + | * Fredman, Komlos, Szemeredi 1984 | ||
| + | * avoid any collisions, O(1) search in a static set | ||
| + | * two-level scheme: use a universal hash function to hash to a table of size m = Theta(n) | ||
| + | * each bucket i with c_i elements hashed to a second-level hash of size Theta(c_i^2) | ||
| + | * again use a universal hash function for each second-level hash | ||
| + | * expected total number of collisions in a second level hash with c_i elements: | ||
| + | ** sum_u,v Pr(h(u) = h(v)) = (c_i)^2 O(1/(c_i)^2) = O(1) | ||
| + | * with a sufficently large constant in second-level hash size we this expected number of collisions to be <=1/2 | ||
| + | * then with probability >=1/2 no collision by Markov inequality | ||
| + | * when building a hash table we get a collision, randomly sample another hash function | ||
| + | * in O(1) expected trials get a good hash function | ||
| + | * expected space: Theta(m + sum_i (c_i^2)) | ||
| + | * sum_i (c_i^2) is the number pairs (x,y) s.t. x,y in T and h(x)=h(y) - include x=y | ||
| + | * sum_{x,y} Pr(h(x)=h(y)) = n + sum_{x!=y} Pr(h(x)=h(y)) = n + n^2 c / m = Theta(n) | ||
| + | * so expected space is linear | ||
| + | |||
| + | Dynamic perfect hashing | ||
| + | * amortized vector-like tricks | ||
| + | * when a 2-nd level hash table get too full, allocate a bigger one | ||
| + | * O(1) deterministic search | ||
| + | * O(1) amortized expectd update | ||
| + | * O(n) expected space | ||
===Bloom Filter (Bloom 1970)=== | ===Bloom Filter (Bloom 1970)=== | ||
Verzia zo dňa a času 22:30, 29. apríl 2015
Zdroje
- Prednaska L10 Erika Demaina z MIT: http://courses.csail.mit.edu/6.851/spring12/lectures/
- Článok z Wikipédia o Bloom filtroch http://en.wikipedia.org/wiki/Bloom_filter
- Učebnica Brass 2008 Advanced data structures
Obsah
Introduction to hashing
- Universe U = {0,..., u-1}
- Table of size m
- Hash function h : U -> {0,...,m-1}
- Let T be the set of elements currently in the hash table, n = |T|
- We will assume n = Theta(m)
Totally random hash function (a.k.a uniform hashing model)
- select hash value h(x) for each x in U uniformy independently
- not practical - storing this hash function requires u * lg m bits
- used for simplified analysis of hashing in ideal case
Universal family of hash functions
- some set of functions H
- draw a fuction h uniformly randomly from H
- there is a constant c such that for any distinct u,v from U we have Pr(h(u) = h(v)) <= c/m
- probability goes over choices of h
Note
- for totally random hash function, this probability is exactly 1/m
Example of a universal family:
- choose a fixed prime p >= u
- H_p = { h_a | h_a(x) =(ax mod p) mod m), 1<=a<=p-1 }
- p-1 hash functions, parameter a chosen randomly
Proof of universality
- consider x!=y, both from U
- if they collide (ax mod p) mod m = (ay mod p) mod m
- let c = (ax mod p), d = (ay mod p)
- note that c,d in {0..p-1}
- also c!=d because otherwise a(x-y) is divisible by p and both a and |x-y| are numbers from {1,...,p-1} and p is prime
- since c mod m = d mod m, then c-d = qm where 0<|qm|<p
- there are <=2(p-1)/m choices of q where |qm|<p
- we get a(x-y) mod p = qm mod p
- this has exactly one solution a in {0...p-1}
- overall at most 2(p-1)/m choices of hash functions collide x and y
- out of p-1 all hash functions in H_p
- therefore probability of collision <=2/m
Hashing with chaining, using universal family of h.f.
- linked list (or vector) for each hash table slot
- let c_i be the length of chain i
- consider element u from U, let i = h(u)
- any element x from T s.t. u!=x maps to i with probability <= c/m
- so E[c_i] <= 1 + n * c / m = O(1)
- from linearity of expectation - sum over indicator variables for each x in T if it collides with u
- +1 in case u is in T
- so expected time of any search, insert and delete is O(1)
- again, expectation taken over random choice of h from universal H
- however, what is the expected length of the longest chain in the table?
- O(1+ sqrt(n^2 / m)) = O(sqrt(n))
- see Brass, p. 382
- there is a matching lower bound
- for totally random hash function this is "only" O(log n / log log n)
- similar bound proved also for some more realistic families of hash functions
- so the worst-case query is on average close to logarithmic
Perfect hashing
- Fredman, Komlos, Szemeredi 1984
- avoid any collisions, O(1) search in a static set
- two-level scheme: use a universal hash function to hash to a table of size m = Theta(n)
- each bucket i with c_i elements hashed to a second-level hash of size Theta(c_i^2)
- again use a universal hash function for each second-level hash
- expected total number of collisions in a second level hash with c_i elements:
- sum_u,v Pr(h(u) = h(v)) = (c_i)^2 O(1/(c_i)^2) = O(1)
- with a sufficently large constant in second-level hash size we this expected number of collisions to be <=1/2
- then with probability >=1/2 no collision by Markov inequality
- when building a hash table we get a collision, randomly sample another hash function
- in O(1) expected trials get a good hash function
- expected space: Theta(m + sum_i (c_i^2))
- sum_i (c_i^2) is the number pairs (x,y) s.t. x,y in T and h(x)=h(y) - include x=y
- sum_{x,y} Pr(h(x)=h(y)) = n + sum_{x!=y} Pr(h(x)=h(y)) = n + n^2 c / m = Theta(n)
- so expected space is linear
Dynamic perfect hashing
- amortized vector-like tricks
- when a 2-nd level hash table get too full, allocate a bigger one
- O(1) deterministic search
- O(1) amortized expectd update
- O(n) expected space
Bloom Filter (Bloom 1970)
- supports insert x, test if x is in the set
- may give false positives, e.g. claim that x is in the set when it is not
- false negatives do not occur
Algorithm
- a bit string B[0,...,m-1] of length m, and k hash functions hi : U -> {0, ..., m-1}.
- insert(x): set bits B[h1(x)], ..., B[hk(x)] to 1.
- test if x in the set: compute h1(y), ..., hk(y) and check whether all these bits are 1
- if yes, claim x is in the set, but possibility of error
- if no, answer no, surely true
Lemma: If hash functions are totally random and independent, the probability of error is at most (1-exp(-nk/m))^k
- proof later
- totally random hash functions impractical (need to store hash value for each element of the universe), but the assumption simplifies analysis
- if we set k = ln(2) m/n, get error
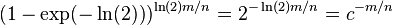 , where
, where 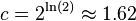
- to get error rate p for some n, we need
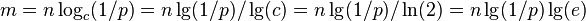
- for 1% error, we need about m=10n bits of space and k=7
- memory size and error rate are independent of the size of the universe U
- compare to a hash table, which needs at least to store data items themselves (e.g. in n lg u bits)
- if we used k=1 (Bloom filter with one hash function), we need m=n/ln(1/(1-p)) bits, which for p=0.01 is about 99.5n, about 10 times more than with 7 hash functions
Use of Bloom filters
- e.g. an approximate index of a larger data structure on a disk - if x not in the filter, do not bother looking at the disk, but small number of false positives not a problem
- Example: Google BigTable maps row label, column label and timestamp to a record, underlies many Google technologies. It uses Bloom filter to check if a combination of row and column label occur in a given fragment of the table
- For details, see Chang, Fay, et al. "Bigtable: A distributed storage system for structured data." ACM Transactions on Computer Systems (TOCS) 26.2 (2008): 4. [1]
- see also A. Z. Broder and M. Mitzenmacher. Network applications of Bloom filters: A survey. In Internet Math. Volume 1, Number 4 (2003), 485-509. [2]
Proof of lemma
- probability that some B[i] is set to 1 by hj(x) is 1/m
- probability that B[i] is not set to 1 is therefore 1-1/m and since we use k independent hash functions, the probability that B[i] is not set to one by any of them is (1-1/m)^k
- if we insert n elements, each is hashed by each function independently of other elements (hash functions are random) and thus Pr(B[i]=0)=(1-1/m)^{nk}
- Pr(B[i]=1) = 1-Pr(B[i]=0)
- consider a new element y which is not in the set
- error occurs when B[hj(y)]==1 for j=1..k,
- this happens with probability Pr(B[i]=1)^k = (1-(1-1/m)^{nk})^k
- recall that for x>1 we have (1-1/x)^x < 1/e (equality in limit as x->infinity)
- thus probability of error <= (1-exp(-nk/m))^k
- In Mitzenmacher & Upfal (2005), pp. 109–111, 308. - less strict independence assumption
Exercise Let us assume that we have separate Bloom filters for sets A and B with the same set k hash functions. How can we create Bloom filters for union and intersection? Will the result be different from filter created directly for the union or for the intersection?
Theory
- Bloom filter above use about 1.44 n lg(1/p) bits to achieve error rate p. There is lower bound of n lg(1/p) [Carter et al 1978], constant 1.44 can be improved to 1+o(1) using more complex data structures, which are then probably less practical
- Pagh, Anna, Rasmus Pagh, and S. Srinivasa Rao. "An optimal Bloom filter replacement." SODA 2005. [3]
- L. Carter, R. Floyd, J. Gill, G. Markowsky, and M. Wegman. Exact and approximate membership testers. STOC 1978, pages 59–65. [4]
- see also proof of lower bound in Broder and Mitzenmacher 2003 below
Counting Bloom filters
- support insert and delete
- each B[i] is a counter with b bits
- insert increases counters, decrease decreases
- assume no overflows, or reserve largest value 2^b-1 as infinity, cannot be increased or decreased
- Fan, Li, et al. "Summary cache: A scalable wide-area web cache sharing protocol." ACM SIGCOMM Computer Communication Review. Vol. 28. No. 4. ACM, 1998. [5]
References
- Bloom, Burton H. (1970), "Space/Time Trade-offs in Hash Coding with Allowable Errors", Communications of the ACM 13 (7): 422–426
- Bloom filter. In Wikipedia, The Free Encyclopedia. Retrieved January 17, 2015, from http://en.wikipedia.org/w/index.php?title=Bloom_filter&oldid=641921171
- A. Z. Broder and M. Mitzenmacher. Network applications of Bloom filters: A survey. In Internet Math. Volume 1, Number 4 (2003), 485-509. [6]
Locality Sensitive Hashing
- Har-Peled, Sariel, Piotr Indyk, and Rajeev Motwani. "Approximate Nearest Neighbor: Towards Removing the Curse of Dimensionality." Theory of Computing 8.1 (2012): 321-350.
- Proprocess: A set P of n binary sequences of length k, radius r, gap c
- Query: binary sequence q of length q
- Output: If there exist a sequence within Hamming distance r from q, find a sequence within r*c of q with probability at least f.
- Hash each point in P using L hashing functions, each using O(log n) randomly chosen sequence positions (hidden constant depends on d, r, c), put all results to bins in one table
- Given q, find it using all L hash function, check every collision, report if distance at most cr. If checked more than 3L collisions, stop.
- L = O(n^{1/c})
- Space O(nL), query time O(Ld+L(d/r)log n)
- Probability of failure less than some constant < 1, can be boosted by repeating independently